2.0 KiB
2.0 KiB
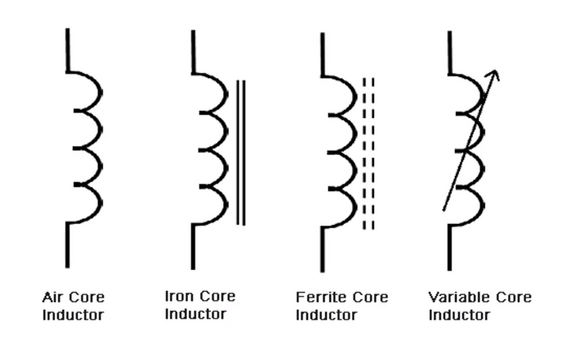
Inductors
Inductors are similar to capacitors, but there are a few key differences:
- They store energy in their magnetic field
- They resist to changes in current
Inductance:
\begin{flalign}
&L = \frac{N^2 * A * \micro}{l} &\\\
\\
&L = Inductance \\
&N = \text{Coil Turns} \\
&A = \text{Area of the coild} \\
&\micro = \text{Permeability} \\
&\textit{How easily a magnetic field can be crated} \\
&l = \text{Length of coil} \\
\end{flalign}
Inductors in Parallel
\displaystyle \frac{1}{L_{t}} =\frac{1}{L_{1}}+\frac{1}{L_{2}}+...+\frac{1}{L_{n}}
Inductive Reactance
Is the strength of opposition to alternating current in an inductor, measured in \ohm
\begin{flalign}
&X_{L} = 2\pi fL&&\\\
&f = Frequency \\
&L = Inductance
\end{flalign}
Example:
$ 1 0.000005 30.13683688681966 45 5 43 5e-11
v 144 256 144 128 0 1 10000 5 0 0 0.5
l 240 128 240 256 0 0.03 -0.004925046545906014 0
w 144 128 240 128 0
w 240 256 144 256 0
o 1 64 0 4099 5 0.025 0 2 1 3
Calculate the Inductive Reactance in this circuit:
\begin{flalign}
&X_{L} = 2\pi fL &\\\
&f = 10kHz = 10.000Hz\\
&L = 30mH = 0.03H\\
&X_{L} = 2\pi * 10.000 * 0.03 \\
&X_{L} \approx 1885\ohm
\end{flalign}
Example 2:
$ 1 0.000005 30.13683688681966 45 5 43 5e-11
v 96 256 96 128 0 1 200 5 0 0 0.5
l 240 128 240 256 0 0.4 0.00896251184146064 0
w 240 256 96 256 0
r 96 128 240 128 0 200
o 1 64 0 4099 5 0.025 0 2 1 3
Calculate the glossary#Impedance Z in this Circuit:
\begin{flalign}
Z = \sqrt{R^2 + X^2} \\
X = X_{L} - {X_{C}} \\
\\
X_{L} = 2\pi fL \\
X_{L} = 2\pi * 200Hz * 400mH \\
X_{L} = 2\pi*200*0.4H\\
X_{L} \approx 502.65\ohm\\
\\
Z = \sqrt{200^2+502.65^2}\\
Z \approx 540.97 \ohm \\
\\
I_{RMS} = \frac{I_{max}}{\sqrt{2}} \\
I_{RMS} = \frac{V_{rms}}{Z} \\
V_{RMS} = \frac{5}{\sqrt{2}} \\
V_{RMS} \approx 3.53V \\
I_{RMS} = \frac{3.53}{540.97} \\
I_{RMS} \approx 6.5mA\\
I_{max} = 0.0065 * \sqrt{2} \\
I_{max} \approx 9.12mA \\
\end{flalign}