2.2 KiB
Impedance/Reactance of capacitors
Capacitive Reactance
Is a measure of a capacitors opposition to alternating current.
Xc in \ohm
$X_{c} = \frac{1}{2 \pi fC}$ $Xc = \textit{Capacity in } \ohm$ f = Frequency in Hertz C = Capacitance in Farads
Higher Frequence \Rightarrow Lower Current Flow
Higher Capacitance \Rightarrow Lower Current Flow
When the Frequency is 0, the capacitor acts as an open circuit When the Frequency is really high, the capacitor is equal to a simple wire
Example:
Calculate the capacitive reactance of a 220nF capacitor at a frequency of 1kHz and 20kHz
\begin{flalign}
&X_{c} = \frac{1}{2 \pi * 1000 * 220 * 10^{-9} } \\
&X_{x} \approx \textbf{723.43} \ohm\\
\\
&X_{c} = \frac{1}{2 \pi * 20000 * 220 * 10^{-9} } \\
&X_{x} \approx \textbf{36.17} \ohm\\
\end{flalign}
Here we can see when the frequency increases the reactive capacitance decreases
Example 2:
$ 1 0.000005 10.20027730826997 50 5 43 5e-11
v 208 256 208 144 0 1 80 5 0 0 0.5
r 208 144 336 144 0 100
c 336 144 336 256 0 0.000029999999999999997 -2.4446139526159825 0.001
w 336 256 208 256 0
How would we calculate the I_{rms} of this circuit, we'll basically using Ohms Formular
I_{rms} = \frac{V_{rms}}{R1+X_{c}}
The Problem is, we can't just simply add up R1 and Xc, because Xc is shifted by 90°. We need to add them up as Vectors:
R_{e} = \sqrt{R1^2+X_{c}^2}
Lets fill in the numbers from the circuit above and test it out:
\begin{flalign}
&X_{c} = \frac{1}{2 \pi * 80 * 30 * 10^{-6}} &&\\\
&X_{c} \approx 66.3 \ohm \\
&V_{rms} = 3.5v \\
\\
&I_{rms} = \frac{3.5}{\sqrt{100^2+66.3^2}} \\
&I_{rms} = \frac{3.5}{119.98} \\
&I_{rms} = 0.029171033 A \\
&I_{rms} \approx 29.17mA
\end{flalign}
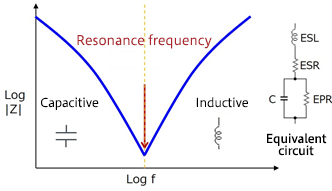
Reality
In reality capacitors are not perfect, they are more like:
So the have a ESR and X_{C} and X_{L} / ESL
C_{IMP} = ESR + X_{C} + X_{L}
Due to this the frequency to impedance curve of real capacitors look something like this.
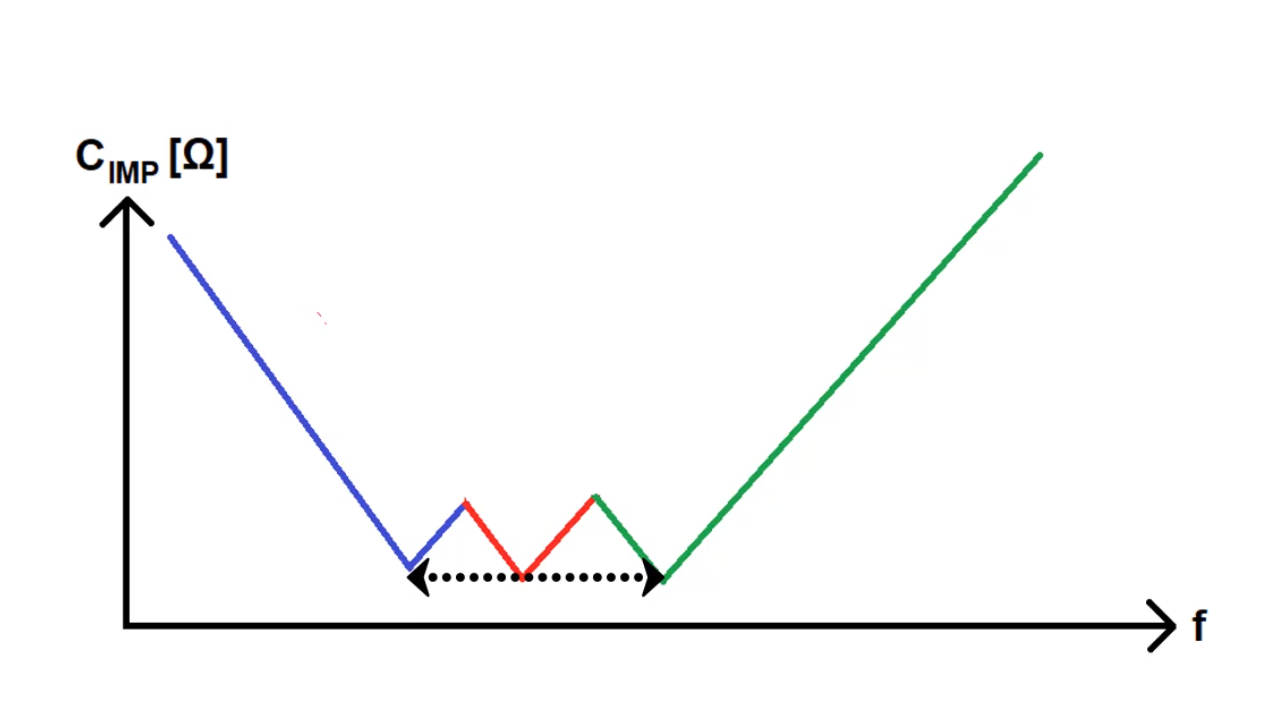
When we add multiple capacitors we can get a curve looking like this